爱尔法鲁酒吧问题python实现，复杂经济学博弈论自组织自适应系统

最近在看布莱恩阿瑟（W.Brian Arthur）的《复杂经济学：经济思想的新框架》时，里面提到的复杂系统的自组织自适应的特点真的很吸引我，其中阿瑟在第二章提出了“爱尔法鲁酒吧问题”，将自适应复杂系统通过一个实验体现了出来，行为主体的每一次决策将影响他们共同存在的环境，而环境又进一步影响行为主体调整自己的决策或行为以适应这个不断因他们而变化的环境，层层递进。

爱尔法鲁酒吧问题简介（The El Farol Bar Problem）

这里我简述一下这个实验的设定，在圣塔菲研究所附近有一家爱尔法鲁酒吧（El Farol），每周四酒吧晚上都会有爱尔兰音乐表演，酒吧空间有限，人多的话整体体验就大打折扣。这里假设小镇有100人，每周四晚上酒吧人数不超过60人的话，就会是一个愉快的晚上，很值得一去；如果酒吧人数超过60人，拥挤吵闹，体验就会很差，还不如留在家中。

而实验要求这些行为主体（即这100个居民）通过归纳推理的方式决定本周四去不去酒吧看表演。经过一段时间后，酒吧的到场人数会不会收敛在一个稳定的水平，这是这个实验要验证的问题。

具体细节我就不再过多赘述，书中的这一章有对应的一篇论文，具体细节可参考这篇论文：《Inductive Reasoning, Bounded Rationality and the Bar Problem》——W. Brian Arthur

代码实现

书和论文中并未提及具体的实现方式，这里就根据书中的描述，使用python来实现（我猜阿瑟是用Basic实现的，因为书里他说那时候他只会Basic语言）。

一个历史人数序列，存放历史到场人数

HISTORY=[]#每周四到场人数

预测器集合，这也是归纳推理的代码体现，只根据历史数据推测本周的人数，书中只提到了六种预测器，这里我还加上了一些自己想到的预测器。

#预测器
class Predictor():
    @staticmethod
    def method1(history=HISTORY):#上周四小于60人就去，否则不去
        if len(history)>0:
            if history[-1]<60:
                return 1
            else:
                return 0
        else:
            return 1

    @staticmethod
    def method2(history=HISTORY):#最近4周的周四平均人数小于60人就去，否则不去
        if len(history)>3:
            days=history[-4:]
            if sum(days)/len(days) < 60:
                return 1
            else:
                return 0
        else:
            return 1

    @staticmethod
    def method3(history=HISTORY):#预测本周四人数与上周四人数以50为中心构成镜像，小于60人就去，否则不去
        if len(history)>0:
            if 100 - history[-1] < 60:
                return 1
            else:
                return 0
        else:
            return 1

    @staticmethod
    def method4(history=HISTORY):#最近8周的周四人数趋势推算，若预测小于60人就去，否则不去
        if len(history)>7:
            days=history[-8:]
            change_rate=sum([days[i]-days[i-1] for i in range(len(days)) if i!=0])/(len(days)-1)
            if days[-1]+change_rate < 60:
                return 1
            else:
                return 0
        else:
            return 1

    @staticmethod
    def method5(history=HISTORY):#上上周四的人数少于60人就去，否则不去
        if len(history)>1:
            the_thursday_before_last=history[-2]
            if the_thursday_before_last<60:
                return 1
            else:
                return 0
        else:
            return 1


    @staticmethod
    def method6(history=HISTORY):#5周前的周四的人数少于60人就去，否则不去
        if len(history)>4:
            the_thursday=history[-5]
            if the_thursday<60:
                return 1
            else:
                return 0
        else:
            return 1

    @staticmethod
    def method7(history=HISTORY):#上周四超过60人，我猜测这周很多人不去，所以我去（我在大气层）
        if len(history)>0:
            if history[-1]>60:
                return 1
            else:
                return 0
        else:
            return 1

    @staticmethod
    def method8(history=HISTORY):#最近2周的周四平均人数大于60人，我猜这周很多人不去，所以我去（我在大气层）
        if len(history)>1:
            last_2_thursdays=history[-2:]
            if sum(last_2_thursdays)/len(last_2_thursdays) > 60:
                return 1
            else:
                return 0
        else:
            return 1


    @staticmethod
    def method9(history=HISTORY):#上上7周的周四平均人数小于60人就去，否则不去
        if len(history)>13:
            days=history[-14:-7]
            if sum(days)/len(days) < 60:
                return 1
            else:
                return 0
        else:
            return 1


    @staticmethod
    def method10(history=HISTORY):#最近7周的周四人数中位数小于60人就去，否则不去
        if len(history)>6:
            days=history[-7:]
            days.sort()
            if days[3] < 60:
                return 1
            else:
                return 0
        else:
            return 1


    @staticmethod
    def method11(history=HISTORY):#最近3周的周四人数，最大值小于60人就去，否则不去
        if len(history)>2:
            days=history[-3:]
            if max(days) < 60:
                return 1
            else:
                return 0
        else:
            return 1

然后写一个函数，将以上的预测器复制三遍，然后随机取二分之一用于后续赋予行为主体，作为它的预测器集合，也可以理解为这个居民所拥有的思维模型或工具箱。

每个预测器都拥有评分，在每次决策后，可以对预测器修改评分，准确就加分，不准确就扣分。

import random
import inspect
import math


#获取打乱的预测器集合： 所有预测器复制三遍，随机打乱，取二分之一，初始准确度都为10。
def getPredictors():
    members=inspect.getmembers(Predictor)
    methods = [member[1] for member in members if inspect.isfunction(member[1]) and not inspect.ismethod(member[1])]
    methods=methods*3
    random.shuffle(methods)
    methods=methods[:math.ceil(len(methods)/2)]
    predictors=[{"method":method, "score":10} for method in methods]
    return predictors

接下来我们实现一个居民模型，一个实例就是一位居民，具体说明我使用代码注释描述。

#居民模型
class Citizen():
    def __init__(self):
        self.predictors=getPredictors()#这个居民所拥有的预测器
        self.last_thursday_arrived=False#上个星期四是否到场，初始值是没有到场
        self.current_predictor=random.choice(self.predictors)#活跃预测器，初始值随机

    #重置某个方法的分数
    def resetPredictorScore(self,the_predictor,score):
        for index,predictor in enumerate(self.predictors):
            if predictor['method']==the_predictor['method']:
                self.predictors[index]['score']=score
                #break #一个人的预测器集合里可能会有同一个预测器出现2-3次的情况，break就是只针对1个处理，不break就是针对所有相同预测器处理

    #选择当前最合适的预测器
    def chooseSuitablePredictor(self):
        predictors = sorted(self.predictors, key=lambda x: x['score'], reverse=True)#将预测器集合根据每个预测器的score从大到小排序
        max_score = max(predictors, key=lambda x: x['score'])['score']
        #candidates=[predictor for predictor in predictors if predictor['score']==max_score]#取最高分的
        candidates=predictors[:4]#取排名前四的 因为同一种预测器最多三份，取前四即允许行为主体出现部分“变异”的可能性
        predictor=random.choice(predictors)
        return predictor


    #决定这个周四去不去
    def decide(self):

        if len(HISTORY)>0:#第一周跳过判断
            last_thursday_num=HISTORY[-1]#上周四人数
            learning_rate=0.1#学习率设置为0.1
            error_rate=abs(last_thursday_num-60)/60#误差率
            #判断错误：如果上周去了且人数超过60人 或者 上周没去且人数没到60，就说明这个预测器失灵 计算误差率 扣分
            if (self.last_thursday_arrived and last_thursday_num>60) or ((not self.last_thursday_arrived) and last_thursday_num<60):
                new_score=self.current_predictor['score']-learning_rate*(1/error_rate)
            else:#判断正确 加分
                if error_rate!=0:
                    new_score=self.current_predictor['score']+learning_rate*(1/error_rate)
                else:
                    new_score=self.current_predictor['score']

            self.resetPredictorScore(self.current_predictor,new_score)#重置某个方法分数

        self.current_predictor=self.chooseSuitablePredictor()#选择自己的预测器集合中的一个作为本周预测方法

        decision=self.current_predictor['method']()#执行预测，获取结果

        if decision==1:#本周四结束 更新上周情况
            self.last_thursday_arrived=True
        elif decision==0:
            self.last_thursday_arrived=False

        return decision

进行实验

以上代码完成了基础工作，接下来我们生成100为居民，并运行100周看看会出现什么情况。

citizens=[Citizen() for i in range(100)]#生成100个居民


#运行一周
def week():
    current_arrived=0#本周四到场人数
    for citizen in citizens:
        current_arrived+=citizen.decide()

    HISTORY.append(current_arrived)


#运行100周
def run100weeks():
    for i in range(100):
        week()


import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['font.family'] = 'sans-serif'
mpl.rcParams['font.sans-serif'] = ['Microsoft Yahei']
#展示人数变化折线图
def showFigure():
    x = [i+1 for i in range(len(HISTORY))]
    y = HISTORY

    plt.plot(x, y)# 绘制折线图

    # 添加标题和标签
    plt.title("酒吧到场人数")
    plt.xlabel("周数")
    plt.ylabel("人数")
    plt.ylim(0, 100) # 设置y轴范围
    plt.yticks(range(0, 101, 10)) # 设置y轴刻度

    plt.show()

打开终端，运行100周看看效果

查看一下折线图，终端中输入showFigure()

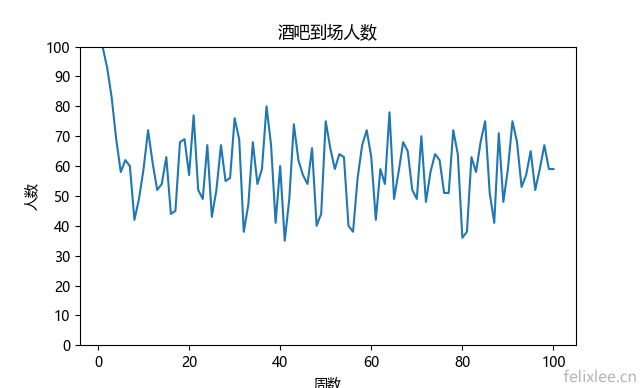
可以观察到，从差不多第10周开始，酒吧每周四到场的人数逐渐收敛到60人附近，在40-80之间波动。这100个行为主体并不知道其他99个这周四到底去不去酒吧，故他们无法通过演绎推理的方式预测本周四的人数，他们只能通过归纳推理，即自己已有的预测器集合，每周选择当前最有效的几个预测器中的一个进行决策，如果预测对了就给这个预测器加分，如果预测错了就给这个预测器扣分，后续转用更有效的预测器。

通过这样一个非常简单的机制，100个行为主体持续影响着它们共同形成的环境，而环境又会反过来影响行为主体的决策，以让行为主体可以更好的适应这个它们共同创造的环境。这是复杂系统的最重要的本质，也是最大的魅力所在。

其他

后面我又尝试了给预测器集合中添加了一些观察长时间变化的预测器，比如观察近15周周四的平均人数，或者观察近15周的中位数，用于判断本周四是否前往酒吧。运行后可以观察到一些剧烈波动的情况，或者说类似经济学中的“泡沫”的情况，人数极高，然后又突然极低，也有出现高峰低谷频繁交替出现的情况。这里就不过多展开，留给大家自行尝试了。

维基百科上找到了这个酒吧的图片，如上图所示，也有看到一些爱尔兰音乐表演的图片，不过现在周四还有没有就不太确定了。

Felix 管理员

推荐阿瑟的另外一本书《技术的本质》，本文提到的《复杂经济学》也是在前者的书末推荐中看到的。这两本书都非常有意思，也没有什么晦涩难懂的东西，阅读起来也不吃力，是了解复杂性科学不错的书籍。

爱尔法鲁酒吧问题python实现，复杂经济学博弈论自组织自适应系统

爱尔法鲁酒吧问题简介（The El Farol Bar Problem）

代码实现

进行实验

其他

Felix 管理员

最新文章

最新随笔